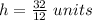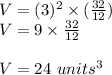Question

A right square prism has a surface area of 50 with each square base having an area of 9. What is the volume of the right square prism

Answer 1

Volume of right square prism =
`24\ units^3`

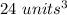
Explanation:

Surface area of right square prism =
`50\ units^2`

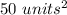
Area of square base =
`9\ units^2`

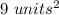
Area of square base is given by =
`a^2`

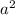
where
`a` represents the square base edge.

So,
`a^2=9`

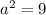
Taking square root both sides.

`\sqrt a^2=\sqrt 9`

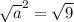
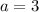`a=3` [ignoring the -3 as we are finding lengths which is always positive]

Surface area of right square prism is given by =
`2a^2+4ah`

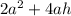
where
`a` represents the square base edge and
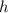`h` represents height of the prism.

So we have,

`2a^2+4ah=50`

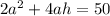
Plugging in values
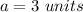`a=3\ units` and surface area=
`50\ units^2`

`2(3)^2+4(3)h=50`

`2(9)+12h=50`

`18+12h=50`

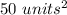
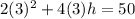
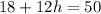
Subtracting both sides by 18.

`18+12h-18=50-18`

`12h=32`

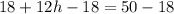
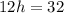
dividing both sides by 12.

`(12h)/(12)=(32)/(12)\\\\h=(32)/(12)\ units`

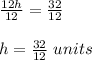
Volume of prism =
`a^2h`

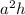
where
`a` represents the square base edge and
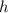`h` represents height of the prism.

Plugging in values
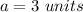`a=3\ units` and
`h=(32)/(12)\ units`

`V=(3)^2*((32)/(12))\\V=9*(32)/(12)\\\\V=24\ units^3`