Question

Let 0 < p < 1. Consider a population of organisms whose lifecycle goes as follows. A newborn individual has probability p of reaching adulthood. Once an adult, the individual gives birth to exactly two offspring, and then dies. Start with a single (adult) individual. Find the probability that this population eventually goes extinct.

Answer 1

Zero

Explanation:

This situation could be modeled with a binomial distribution.

After n generations, the probability that there are exactly k adults would be

`\large\bf \binom{n}{k}p^k(1-p)^(n-k)`

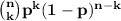
So, the probability that there are no adults after n generations is

`\large\bf \binom{n}{0}p^0(1-p)^(n)=(1-p)^n`

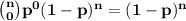
The population would eventually go extinct if

`\large\bf \lim_(n \rightarrow \infty)(1-p)^n=1`

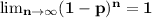
But, 0 < p < 1 as a consequence 0 < 1-p <1 and

`\large\bf \lim_(n \rightarrow \infty)(1-p)^n=0`

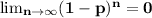
Hence, the probability that the organism will go extinct is 0.