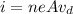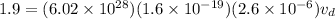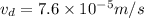Question

An aluminium wire with a cross-sectional area of 2.6 × 10−6 m2 carries a current of 1.9 A . Find the drift speed of the electrons in the wire. Assume that each atom supplies one electron. Aluminium has a molecular weight of 26.98 g/mol and a density of 2.7 g/cm3 . Avogadro’s number is 6.022 × 1023 and the fundamental charge is 1.602 × 10−19 C . Answer in units of m/s.

Answer 1

`v_d = 7.6 * 10^(-5) m/s`

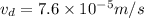
Step-by-step explanation:

As we know that electric current is given as

`i = neA v_d`

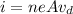
here we know that

`A = 2.6 * 10^(-6) m^2`

i = 1.9 A

`e = 1.6 * 10^(-19) C`

Molar mass of the wire is

M = 26.98 g/mol

density of the wire is

`\rho = 2.7 g/cm^3`

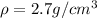
now let the mass of the wire is M gram

so number of atoms of Al in the wire is given as

`N = (M)/(26.98)(6.02 * 10^(23))`

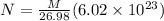
now number density is given as

`n = (N)/(V)`

`n = (\rho)/(26.98)(6.02 * 10^(23))`

`n = 6.02 * 10^(22) per cm^3`

`n = 6.02 * 10^(28) per m^3`

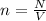
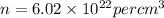
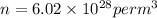
now we will have

`i = neAv_d`

`1.9 = (6.02 * 10^(28))(1.6 * 10^(-19))(2.6 * 10^(-6))v_d`

`v_d = 7.6 * 10^(-5) m/s`