Question

A sanding disk with rotational inertia 2.0 x 10-3 kg·m2 is attached to an electric drill whose motor delivers a torque of magnitude 32 N·m about the central axis of the disk. About that axis and with torque applied for 62 ms, what is the magnitude of the(a) angular momentum and(b) angular velocity of the disk?

Answer 1

Step-by-step explanation:

It is given that,

Moment of inertia of a standing disk,
`I=2* 10^(-3)\ kg.m^2`

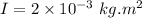
Torque acting on the motor,
`\tau=32\ N.m`

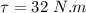
Time for which the torque is applied,
`t=62\ ms=62* 10^(-3)\ s`

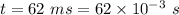
(a) The relationship between the angular momentum and the torque is given by :

`\tau=(dL)/(dt)`

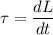
Where

L is the angular momentum of the disk

`L=\tau* t`

`L=32\ N.m* 62* 10^(-3)\ s`

`L=1.984\ kg.m^2/s`

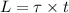
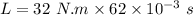
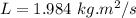
(b) Let
`\omega` is the angular velocity of the disk. The relation between the angular velocity and the angular momentum is given by :

`L=I* \omega`

`\omega=(L)/(I)`

`\omega=(1.984)/(2* 10^(-3))`

`\omega=990\ rad/s`

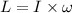
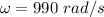
Hence, this is the required solution.