Question

An experiment is conducted on a long straight wire of diameter d. A constant current is sent through the wire and the magnetic field on the surface of the wire is measured to be B1. The experiment is then repeated with the same current but with a wire of diameter 2d. The magnetic field measured on the surface of this second wire will be which of the following?a. B1, b. B1 / 4, c. 4B1, d. B1 / 2

Answer 1

D.

Step-by-step explanation:

To solve the exercise it is necessary to apply the concepts related to the Magnetic Field described by Faraday.

The magnetic field is given by the equation:

`B = (\mu_0 I)/(2\pi d)`

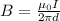
Where,

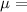`\mu =` Permeability constant

d = diameter

I = Current

For the given problem we have a change in the diameter, twice that of the initial experiment, therefore we define that:

`B_1 = (\mu_0 I)/(2\pi d)`

`B_2 = (\mu_0 I)/(2\pi 2d)`

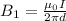
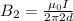
The ratio of change between the two is given by:

`(B_2)/(B_1) = ((\mu_0 I)/(2\pi d))/((\mu_0 I)/(2\pi 2d))`

`(B_2)/(B_1) = (d)/(2d)`

`(B_2)/(B_1) = (1)/(2)`

`B_2 = B_1 (1)/(2)`

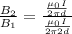
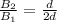
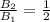
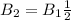
Therefore the correct answer is D.