Question

A closely wound search coil has an area of 3.21 cm2, 120 turns, and a resistance of 58.7 O. It is connected to a charge-measuring instrument whose resistance is 45.5 O. When the coil is rotated quickly from a position parallel to a uniform magnetic field to one perpendicular to the field, the instrument indicates a charge of 3.53 x 10-5 C.What is the magnitude of the magnetic field?

Answer 1

The magnetic field in the System is 0.095T

Step-by-step explanation:

To solve the exercise it is necessary to use the concepts related to Faraday's Law, magnetic flux and ohm's law.

By Faraday's law we know that

`\epsilon = (NBA)/(t)`

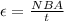
Where,

`\epsilon  =`electromotive force

N = Number of loops

B = Magnetic field

A = Area

t= Time

For Ohm's law we now that,

V = IR

Where,

I = Current

R = Resistance

V = Voltage (Same that the electromotive force at this case)

In this system we have that the resistance in series of coil and charge measuring device is given by,

`R = R_c + R_d`

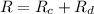
And that the current can be expressed as function of charge and time, then

`I = (q)/(t)`

Equation Faraday's law and Ohm's law we have,

`V = \epsilon`

`IR = (NBA)/(t)`

`((q)/(t))(R_c+R_d) = (NBA)/(t)`

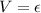
Re-arrange for Magnetic Field B, we have

`B = (q(R_c+R_d))/(NA)`

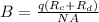
Our values are given as,

`R_c = 58.7\Omega`

`R_d = 45.5\Omega`

`N = 120`

`q = 3.53*10^(-5)C`

`A = 3.21cm^2 = 3.21*10^(-4)m^2`

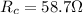
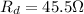
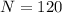
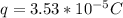
Replacing,

`B = ((3.53*10^(-5))(58.7+45.5))/(120*3.21*10^(-4))`

`B = 0.095T`

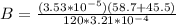
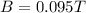
Therefore the magnetic field in the System is 0.095T