Question

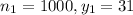
A researcher finds that of 1000 people who said that they attend a religious service at least once a week, 31 stopped to help a person with car trouble. Of 1200 people interviewed who had not attended a religious service at least once a month, 22 stopped to help a person with car trouble. At the 0.05 significance level, test the claim that the two proportions are different.

Answer 1

Out of 1000 people who said that they attend a religious service at least once a week, 31 stopped to help a person with car trouble

`n_1=1000 , y_1=31`

Of 1200 people interviewed who had not attended a religious service at least once a month, 22 stopped to help a person with car trouble.

`n_2=1200 , y_2=22`

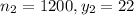
We will use Comparing Two Proportions

`\widehat{p_1}=(y_1)/(n_1)`

`\widehat{p_1}=(31)/(1000)`

`\widehat{p_1}=0.031`

`\widehat{p_2}=(y_2)/(n_2)`

`\widehat{p_2}=(22)/(1200)`

`\widehat{p_2}=0.0183`

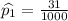
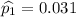
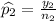
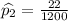
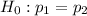`H_0:p_1=p_2`i.e. religion service makes no difference

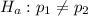`H_a:p_1 \\eq p_2` i.e. religion service makes difference

`\widehat{p}=(y_1+y_2)/(n_1+n_2)=(31+22)/(1000+1200) =0.024`

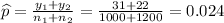
Formula of test statistic :
`\frac{\widehat{p_1}-\widehat{p_2}}{\sqrt{\widehat{p}(1-\widehat{p})((1)/(n_1)+(1)/(n_2))}}`

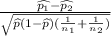
Substitute the values

test statistic :
`\frac{0.031-0.0183}{\sqrt{0.024(1-0.024)((1)/(1000)+(1)/(1200))}}= 1.937`

Refer the z table for p value

p value = 0.9726

α=0.05

p value >α

So, we failed to reject null hypothesis

Hence religion service makes no difference