Answer:
The answer is:
As x decreases without bound, the graph of f(x) approaches y = 0
As x increases without bound, the graph of f(x) increases without bound
Explanation:
When x goes -∞;

When x goes to ∞;
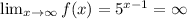
Therefore the solution is;
As x decreases without bound, the graph of f(x) approaches y = 0
As x increases without bound, the graph of f(x) increases without bound