Question

A 4-kg mass moving with speed 2 m/s, and a 2-kg mass moving with a speed of 4 m/s, are gliding over a horizontal frictionless surface. Both objects encounter the same horizontal force, which directly opposes their motion, and are brought to rest by it. Which statement best describes their respective stopping distances?

A) Both masses travel the same distance before stopping.
B) The 2-kg mass travels twice as far as the 4-kg mass before stopping
C) The 2 kg mass travels greater than twice as far
D) The 4-kg mass travels twice as far as the 2-kg mass before stopping

Answer 1

B) The 2-kg mass travels twice as far as the 4-kg mass before stopping

Step-by-step explanation:

As we know that both mass have same horizontal force opposite to their motion

So we will have

`a = (F)/(m)`

`a_1 = (F)/(4)`

`a_2 = (F)/(2)`

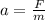
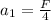
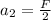
now the stopping distance of an object moving with initial speed v is given as

`v_f^2 - v_i^2 = 2(-a) d`

`d = (v^2)/(2a)`

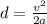
so here we have

`d_1 = (2^2)/((F)/(4))`

`d_1 = (16)/(F)`

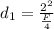
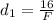
for other object we have

`d_2 = (4^2)/((F)/(2))`

`d_2 = (32)/(F)`

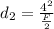
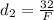
So correct answer will be

B) The 2-kg mass travels twice as far as the 4-kg mass before stopping