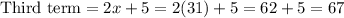Question

Answer please!!!!!!!!!

Answer 1

Third term is 67.

Explanation:

Let the first term of the sequence be
`x`.

Given:

The second term is 5 more than the first term.

Second term =
`x+5`

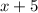
Third term = First term + Second term =
`x+x+5=2x+5`

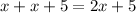
Fourth term = Second term + Third term =
`x+5+2x+5=3x+10`

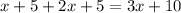
Sum of first 4 terms is 237. Therefore,

`x+(x+5)+(2x+5)+(3x+10)=237\\(x+x+2x+3x) + (5+5+10)=237.........(\textrm{Commutative property of addition})\\7x+20=237\\7x=237-20\\7x=217\\x=(217)/(7)=31`

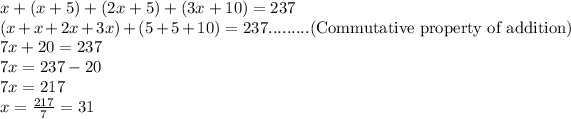
Now, the third term of the sequence is given as:

`\textrm{Third term}=2x+5=2(31)+5=62+5=67`