Question

If I add the square of a number to

2 times the number, I get 63.
What could the number be?

Answer 1

`</p><p>x^2+2x=63 \\</p><p>x^2+2x-63=0 \\</p><p>(x+9)(x-7)=0 \\</p><p>\boxed{x_1=-9,x_2=7}</p><p>`

Hope this helps.

Answer 2

If I add the square of a number to 2 times the number, I get 63. The number can be 7 or -9

Solution:

Given that if i add the square of a number to 2 times the number, i get 63

We have to find the number.

Let the number be "n"

Square of number + 2 times the number = 63

Hence we get,

`n^2 + 2n = 63\\\\n^2 + 2n - 63 = 0`

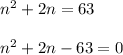
Let us factorize the expression

`n^2 + 2n - 63 = 0`

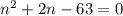
"2n" can be written as "-7n + 9n"

`n^2 -7n + 9n - 63 = 0`

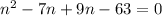
Now 63 can be written as "9 x 7"

`n^2 -7n + 9n - (9 * 7) = 0`

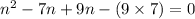
Take "n" as common term from two terms and "9" as common from last two term

`n(n - 7) + 9(n - 7) = 0`

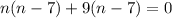
Now take "n - 7" as common term

`(n-7)(n + 9) = 0`

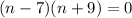
Equating to zero we get,

n - 7 = 0 or n + 9 = 0

n = 7 or n = -9

Hence the number can be 7 or -9