Question

A line passes through (2,4) and (-2,2). find the value of y if (6,y) lies on the same line

Answer 1

y=6

Explanation:

Find the slope

take one point and the slope and insert in the "point-slope"

then solve for y

answer 6

Answer 2

y = 6, rendering the coordinate pair: (6,6)

Explanation:

We start by writing the equation of the line that passes through two given points on the plane:
`(x_1,y_1)` and
`(x_2,y_2)` beginning with finding the slope of the segment that joints the points using the slope formula:
`slope=(y_2-y_1)/(x_2-x_1)`

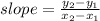
Let's call
`(x_1,y_1)` = (2,4), and
`(x_2,y_2)` = (-2,2). Then we have the formula for the slope:

`slope=(y_2-y_1)/(x_2-x_1)=(2-4)/(-2-2) =(-2)/(-4) =(1)/(2)`

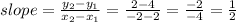
Now that we have the slope of the line, we can find the actual equation of the line by using one of the given points, and the "point-slope" form of a line with slope "m" and going through a point
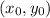`(x_0,y_0)` - which in our case we defie as one of our given points, let's say (2, 4):

`y-y_0=m\,(x-x_0)\\y-4=(1)/(2) (x-2)\\y-4=(1)/(2) x-1\\y=(1)/(2) x-1+4\\y=(1)/(2) x+3`

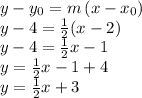
now we find what is the "y" value in such line that corresponds to an x-value of "6" to complete the coordinate pair (6, ?). For such we simply evaluate the equation above at x = 6:

`y=(1)/(2) x+3\\y=(1)/(2) (6)+3\\y=3+3\\y=6`

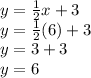
Therefore, y must be "6".