Answer:
The required verification is given below.
Explanation:
To verify:

Consider,
Left hand side =

Now by using Trigonometric identities,
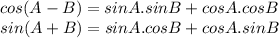
Now we get,
Left hand side =
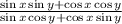
Now dividing Numerator and Denominator by
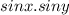 we get
we get
Left hand side =

Now we have identity
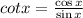
and
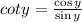 then
then
Left hand side =
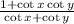
Which is equal to our Right hand side required identity
This is the way we have
Left hand side = Right hand side Proved.