Question

The perimeter of a rectangle is 64 feet. Describe the possible lengths of a side if the area of the rectangle is not to exceed 207 square feet.

Answer 1

Length of Rectangle is 23 feet and width is 9 feet.

Explanation:

Given:

Area of rectangle = 207 square feet

Perimeter of rectangle = 64 feet

We need to find length l and width w.

Solution:

Perimeter of Rectangle =
`2*(length+width) =2(l+w)\\`

Substituting the given values we get,

`64= 2(l+w)\\l+w =(64)/(2)=32\\\therefore<strong> l =32- w</strong>`

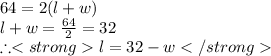
Now, Area of Rectangle =
`length* width=l* w\\`

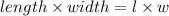
Substituting Values of Area and length we get

`(32-w)* w =207\\32w-w^2=207\\w^2-32w-207=0\\w^2-9w-32w-207=0\\w(w-9)-32(w-9)=0\\(w-9)(w-32)=0`

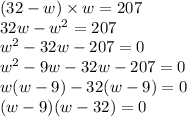
Solving for both equation we get,

`w-9=0\\w=9\\w-23=0\\w=23`

Now we get 2 values for width, let us assume 1 value which is lower as width is always lower than length

so width w = 9 feet

length l =
`32 -w =32-9=23 \ feet`

Length of Rectangle is 23 feet and width is 9 feet.