Question

A movie theatre Has a seating capacity of 165. The theater charges five dollars for children seven dollars for students and $12 for adults. There are half as many adults as there are children. If the total ticket sales was $1182 how many children students and adults attended?

Answer 1

The number of children are 54, number of students are 84 and number of adults are 27.

Explanation:

Let the number of children be
`x`

Let the number of students be
`y`

Let the number of adults be
`z`

As per question,

`x+y+z=165\\5x+7y+12z=1182`

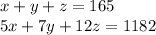
Now, adults are half of the children.

So,
`z=(x)/(2)\\x=2z`

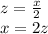
Now, plug in
`x=2z` in the first two equations.

`2z+y+z=165\\3z+y=165-----------------3\\\\ 5(2z)+7y+12z=1182\\10z+12z+7y=1182\\7y+22z=1182 ---------------- 4`

Multiply equation (3) by -7 and add it to equation (4).

`(3z+y=165)* -7=-21z-7y=-1155\\\\-21z-7y+7y+22z=-1155+1182\\(22z-21z)+(7y-7y)=27\\z=27`

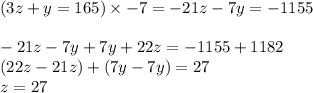
Solve for the remaining variables.

`x=2z=2* 27=54`

`x+y+z=165\\54+y+27=165\\81+y=165\\y=165-81=84`

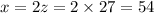
Therefore, the number of children are 54, number of students are 84 and number of adults are 27.