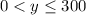Answer:
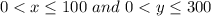
Explanation:
Given:
Maximum number of out-of-state students,
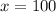
Maximum number of in-state students,
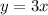
Therefore, the range of out-of-state students can be anywhere between a number greater than 0 but less than or equal to 100 as this is maximum limit.
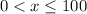
In order to get the interval for
 , we multiply the above by 3 throughout.
, we multiply the above by 3 throughout.
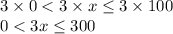
But
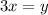 . Therefore,
. Therefore,