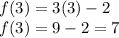Answer:

Explanation:
Given:


0 -2
2 4
6 16
Let us first determine whether the rate of change of the function is constant or not.
The rate of change of the function is given as:
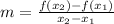
So, for

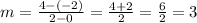
For the next set of numbers,
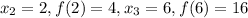
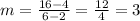
Therefore, the rate of change of the function is a constant. Therefore, the relationship is a linear relationship.
A linear relationship with a given point
 and constant rate of change
and constant rate of change
 is given as:
is given as:
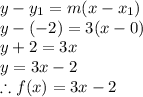
Now, value of
 is obtained by plugging in 3 for
is obtained by plugging in 3 for
 in the above expression.
in the above expression.