Question

A pole that is 2.5 m tall casts a shadow that is 1.47 m long. At the same time, a nearby tower casts a shadow that is 36.25 m long. How tall is the tower? Round your answer to the nearest meter. Show work as well.

Answer 1

The tower is 61.65 meters tall.

SOLUTION:

Given that, a pole that is 2.5 m tall casts a shadow that is 1.47 m long.

At the same time, a nearby tower casts a shadow that is 36.25 m long.

We have to find height of the tower.

Now, we know that,

`2.5 \mathrm{m} \text { tall } \rightarrow 1.47 \text { long shadow }`

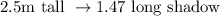
Then, (let it be) n meter tall
`\rightarrow` 36.25 long shadow

So, by cross multiplication method,

`\Rightarrow (2.5)/(1.47)=(n)/(36.25)`

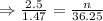
This can be written as,

`\Rightarrow 36.25 * 2.5=1.47 * n \rightarrow 1.47 n=90.625 \rightarrow n=61.649 \rightarrow n=61.65 \text{ m}`

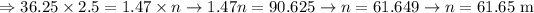
Cross multiplications steps: (To find Single Variable)

1. Multiply the numerator of the left-hand fraction by the denominator of the right-hand fraction.
2. Multiply the numerator of the right-hand fraction by the denominator of the left-hand fraction.
3. Set the two products equal to each other.
4. Solve for the variable.