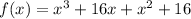Question

How to find a polynomial with the given zeros of -1 and 4i

Answer 1

`f(x) = {x}^(3) + 16x + {x}^(2) + 16`

Explanation:

We want to find the polynomial function whose zero are -1 and 4i.

Recall that non-real zeros come in pairs.

There if 4i is a zero, then the conjugate -4i is also a zero.

Therefore the factors of this polynomial are:

x+1, x+4i, and x-4i are factors of the given polynomial.

Let f(x) be the required polynomial, then we can write the polynomial in factored form as:

`f(x) = (x + 1)(x - 4i)(x + 4i)`

We expand the conjugate pair using difference of two squares to get:

`f(x) =(x + 1) ( {x}^(2) - {(4i)}^(2) )`

`f(x) =(x + 1) ( {x}^(2) + 16)`

Expand further using the distributive property to get:

`f(x) = {x}^(3) + 16x + {x}^(2) + 16`