Question

If A - B = 41°, find the degree measure of angle A when tanA + tanB + tanAtanB = 1. A and B are both acute angles.

Answer 1

The value of angle A is 43° and

The value of angle B is 2° .

Explanation:

Given as :

A - B = 41° .....1

And , tan A + tan B + tan A tan B = 1

Or, tan A + tan B = 1 - tan A tan B ....2

∵ tan ( A + B ) =
`(tan A + tan B)/(1 - tan A tan B)`

Or, tan ( A + B ) =
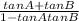
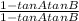`(1 - tanAtanB)/(1 - tanAtanB)` (from eq 2)

∴ tan ( A + B ) = 1

A + B =
`tan^(-1)1`

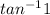
I.e A + B = 45° ........3

Now, from eq 1 and eq 3

A - B = 41°

A + B = 45°

Or, ( A - B ) + ( A + B ) = 41° + 45°

Or, 2 A = 86°

∴ A =
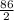`(86)/(2)` = 43°

Now, putting the value of angle A in eq 1

I.e A - B = 41°

Or, B = 43° - 41° = 2°

Hence The value of angle A is 43° and The value of angle B is 2° . Answer