Answer:
The acceleration of a point on the wheel is 11.43 m/s² acting radially inward.
Step-by-step explanation:
The centripetal acceleration acts on a body when it is performing a circular motion.
Here, a point on the bicycle is performing circular motion as the rotation of the wheel produces a circular motion.
The centripetal acceleration of a point moving with a velocity
 and at a distance of
and at a distance of
 from the axis of rotation is given as:
from the axis of rotation is given as:
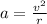
Here,
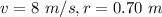
∴
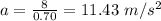
Therefore, the acceleration of a point on the wheel is 11.43 m/s² acting radially inward.