Question

Use the Mean Value Theorem to prove that if the derivative of f(x) is less than or equal to 2 for x>0 and f(0)=4 then f(x) is less than or equal to 2x+4 for all x greater than or equal to 0.

Answer 1

The proof is given below.

Explanation:

Given:

`f'(x)\leq 2,\ f(0)=4, \ x>0`

Using Mean Value Theorem,

`f'(c)=(f(b)-f(a))/(b-a)`

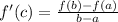
Here,
`a=0,\ b=x`

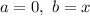
Therefore,
`f'(c)=(f(x)-f(0))/(x-0)=(f(x)-4)/(x)`

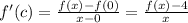
Now, as per question the derivative of
`f(x)` is less than or equal to 2.

Therefore,
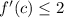`f'(c)\leq 2`. Plug in the value of
`f'(c)`. This gives,

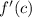`(f(x)-4)/(x)\leq 2\\f(x)-4\leq 2x ...............(\textrm{Cross product})\\f(x)\leq 2x+4 ..............(\textrm{Adding 4 both sides})`

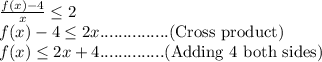
Therefore, we get,
`f(x)\leq 2x+4` and hence it is proved using mean value theorem.