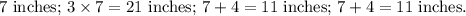Question

The perimeter of a quadrilateral (four-sides polygon) is 50 inches. The longest side is three times as long as the shortest side. The other two sides are equally long and are 4 inches longer than the shortest side. Find the length of all four sides.

Answer 1

The side lengths of quadrilateral are 21 inches; 11 inches; 11 inches; 7 inches.

SOLUTION:

Given, the perimeter of a quadrilateral (four-side polygon) is 50 inches.

Let the length of shortest side be n inches. The longest side is three times as long as the shortest side.

That is, length of largest side = 3n inches

The other two sides are equally long and are 4 inches longer than the shortest side.

Then, length of remaining two sides = 4 + n inches

We have to find the length of all four sides.

Now, we know that, perimeter = 50 inches

`\begin{array}{l}{\rightarrow \text { Sum of all sides }=50} \\\\ {\rightarrow n+3 n+n+4+n+4=50} \\\\ {\rightarrow n+3 n+n+n=50-4-4} \\\\ {\rightarrow 6 n=42} \\\\ {\rightarrow n=7}\end{array}`

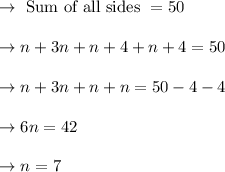
So, length of sides will be,

`7 \text { inches; } 3*7=21 \text { inches; } 7+4=11 \text { inches; } 7+4=11 \text { inches. }`