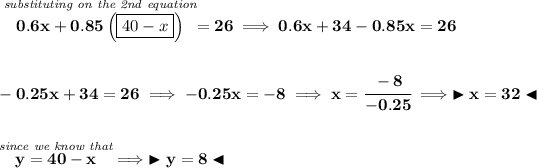Question

A scientist has two solutions, which she has labeled Solution A and Solution B. Each contains salt. She knows that Solution A is 60 % salt and Solution B is 85 % salt. She wants to obtain 40 ounces of a mixture that is 65 % salt. How many ounces of each solution should she use?

Answer 1

x = amount of ounces in first substance

y = amount of ounces in second substance

well, we know that substance A has "x" ounces and has 60% of salt, so the total amount of salt in A will just be 60% of "x" or namely 0.60x.

likewise for the substance B, 85% of "y" will just be 0.85y.

we know that if we add those ounces we'll end up with a mixture of 40 ounces, thus x + y = 40, and their combined pure salt amounts will also be 0.6x + 0.85y, so let's proceed.

`\bf \begin{array}{lcccl} &\stackrel{solution}{quantity}&\stackrel{\textit{\% of }}{amount}&\stackrel{\textit{oz of }}{amount}\\ \cline{2-4}&\\ A&x&0.6&0.6x\\ B&y&0.85&0.85y\\ \cline{2-4}&\\ mixture&40&0.65&26 \end{array}~\hfill \begin{cases} x+y=40\\ \boxed{y} = 40 -x\\[-0.5em] \hrulefill\\ 0.6x+0.85y=26 \end{cases} \\\\[-0.35em] ~\dotfill`

`\bf \stackrel{\textit{substituting on the 2nd equation}}{0.6x+0.85\left(\boxed{40-x} \right)}=26\implies 0.6x+34-0.85x=26 \\\\\\ -0.25x+34=26\implies -0.25x=-8\implies x = \cfrac{-8}{-0.25}\implies \blacktriangleright x = 32 \blacktriangleleft \\\\\\ \stackrel{\textit{since we know that}}{ y = 40 -x }\implies \blacktriangleright y = 8 \blacktriangleleft`