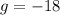Question

5/9(g + 18) = 1/6g +3​

Answer 1

For this case we have the following equation:

`\frac {5} {9} (g + 18) = \frac {1} {6} g + 3`

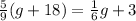
Applying distributive property on the left side of the equation we have:

`\frac {5} {9} g + \frac {5 * 18} {9} = \frac {1} {6} g + 3\\\frac {5} {9} g + \frac {90} {9} = \frac {1} {6} g + 3\\\frac {5} {9} g + 10 = \frac {1} {6} g + 3`

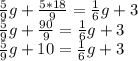
Subtracting
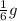`\frac {1} {6} g` to both sides of the equation:

`\frac {5} {9} g- \frac {1} {6} + 10 = 3\\\frac {6 * 5-9 * 1} {9 * 6} g + 10 = 3\\\frac {30-9} {54} g + 10 = 3\\\frac {21} {54} g + 10 = 3\\\frac {7} {18} g + 10 = 3`

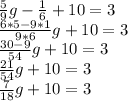
Subtracting 10 to both sides of the equation:

`\frac {7} {18} g = 3-10\\\frac {7} {18} g = -7`

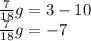
Multiplying by 18 on both sides:

`7g = -7 * 18\\7g = -126`

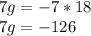
Dividing between 7 on both sides:

`g = \frac {-126} {7}\\g = -18`

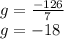
Thus, the value of g is -18.

ANswer:

`g = -18`