Answer:
2.4 years
Explanation:
We can write two equations for each Type and equate and solve for unknown variable.
First, we need to make the initial height (in ft) to inches.
Type A:
3 feet = 3 * 12 = 36 inches
Type B:
4 feet = 4 * 12 = 48 inches
Let "t" be the number of years
For Type A, the equation would be:
36 + 15t [36 inches already and 15 inches per year]
For Type B, the equation would be:
48 + 10t [48 inches and 10 inches per year]
Now we equate and solve for "t", the time when both are same height:
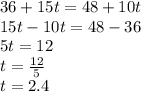
Hence, after 2.4 years, both trees' heights would be same