Question

Which is the graph of f(x) = (2)-x ?

On a coordinate plane, an exponential function approaches y = 0 in quadrant 2 and increases into quadrant 1. It crosses the y-axis at (0, 1).

On a coordinate plane, an exponential function approaches y = 0 in quadrant 1 and increases into quadrant 2. It crosses the y-axis at (0, 1).

On a coordinate plane, an exponential function approaches y = 0 in quadrant 1 and increases into quadrant 2. It crosses the y-axis at (0, 2).

Answer 1

The correct option is B) On a coordinate plane, an exponential function approaches y = 0 in quadrant 1 and increases into quadrant 2. It crosses the y-axis at (0, 1).

Explanation:

Consider the provided equation.

`f(x) = (2)^(-x)`

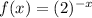
Draw the graph of the equation by using the table shown below:

x f(x)

-2 4

-1 2

0 1

1 0.5

2 0.25

Now draw the graph by using the table.

By observe the graph the exponential function approaches y = 0 in quadrant 1.

The function increases into quadrant 2 and It crosses the y-axis at (0, 1).

Hence, the correct option is B) On a coordinate plane, an exponential function approaches y = 0 in quadrant 1 and increases into quadrant 2. It crosses the y-axis at (0, 1).

Answer 2

We will choose option 2.

Explanation:

The given function is
`f(x) = 2^(-x) = (1)/(2^(x) )`

So, from the above equation it is clear that as x increases in the first quadrant the value of f(x) tends to zero and increases into second quadrant.{ Since x is negative in the second quadrant}

Again, for x = 0, y becomes 1, i.e. the function crosses the y axis at (0,1).

Therefore, on a coordinate plane, an exponential function approaches y = 0 in quadrant 1 and increases into quadrant 2. (0, 1) point is the point of intersection with the y-axis.

So, we will choose option 2. (Answer)