well, let's keep in mind that perpendicular lines have negative reciprocal slopes, so hmmm wait a second, what's the slope of the equation above anyway?
![\bf 9x+3y=15\implies 3y=-9x+15\implies y=\cfrac{-9x+15}{3}\implies y=\cfrac{-9x}{3}+\cfrac{15}{3} \\\\\\ y=\stackrel{\stackrel{m}{\downarrow }}{-3}x+5\qquad \impliedby \begin{array}ll \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array} \\\\[-0.35em] ~\dotfill](https://img.qammunity.org/2020/formulas/mathematics/middle-school/8dkrtqcyi7dju96ngffl5f8q2n2q1mmz5f.png)
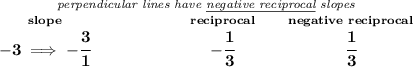
so then, we're really looking for the equation of a line whose slope is 1/3 and runs through (-3,3)
![\bf (\stackrel{x_1}{-3}~,~\stackrel{y_1}{3})~\hspace{10em} \stackrel{slope}{m}\implies \cfrac{1}{3} \\\\\\ \begin{array}c \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{3}=\stackrel{m}{\cfrac{1}{3}}[x-\stackrel{x_1}{(-3)}] \\\\\\ y-3=\cfrac{1}{3}(x+3)\implies y-3=\cfrac{1}{3}+1\implies y=\cfrac{1}{3}x+4](https://img.qammunity.org/2020/formulas/mathematics/middle-school/1l5q094api425li6xt8gop1g3jo36jrexq.png)