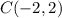Answer:
The point that divides the line AB in the ration 2 : 1 is
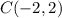
Explanation:
Given:
Point
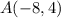 and point
and point
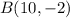
Point
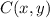 lies in between of AB such that
lies in between of AB such that
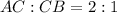
Using section formula which says that, when a point P divided a line AB in the ratio
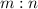 , then the co-ordinates of the point P are:
, then the co-ordinates of the point P are:
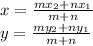
Here,
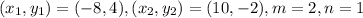
Therefore, the
 and
and
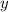 values of point C are:
values of point C are:
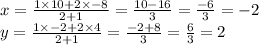
Therefore, the point that divides the line AB in the ration 2 : 1 is