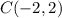Question

Again i hope you can see the picture if you can’t let me know but if you can please help!

Answer 1

The point that divides the line AB in the ration 2 : 1 is
`C(-2,2)`

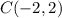
Explanation:

Given:

Point
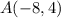`A(-8, 4)` and point
`B(10, -2)`

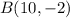
Point
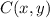`C(x,y)` lies in between of AB such that
`AC : CB = 2 : 1`

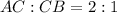
Using section formula which says that, when a point P divided a line AB in the ratio
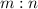`m : n`, then the co-ordinates of the point P are:

`x=(mx_2+nx_1)/(m+n)\\y=(my_2+ny_1)/(m+n)`

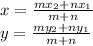
Here,
`(x_1,y_1)=(-8,4),(x_2,y_2)=(10,-2),m=2,n=1`

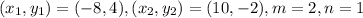
Therefore, the
`x` and
`y` values of point C are:

`x=(1* 10+2* -8)/(2+1)=(10-16)/(3)=(-6)/(3)=-2\\y=(1* -2+2* 4)/(2+1)=(-2+8)/(3)=(6)/(3)=2`

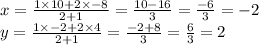
Therefore, the point that divides the line AB in the ration 2 : 1 is
`C(-2,2)`