Answer:
The graph in the attached figure
Explanation:
we have
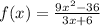
Remember that the denominator cannot be equal to zero
so
The value of x cannot be equal to x=-2
Simplify the numerator
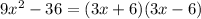 ----> by difference of squares
----> by difference of squares
substitute
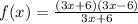
simplify

The domain is all real numbers except the value of x=-2
The y-intercept is the point (0,-6) ---> value of y when the value of x is equal to zero)
The x-intercept is the point (2,0) ---> value of x when the value of y is equal to zero)
therefore
The graph in the attached figure