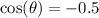Question

Given that sin θ ≈ −0.866, where π < θ < 3 , 2 π find cos θ.

Answer 1

`\cos( \theta) = - 0.5`

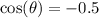
Explanation:

It was given that sin θ ≈ −0.866.

To find cosθ, we apply the Pythagorean property;

`\cos^(2) ( \theta) + \sin^(2) ( \theta) = 1`

`\implies \cos^(2) ( \theta) = 1 - \sin^(2) ( \theta)`

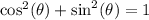
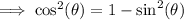
We substitute the given value to get:

`\cos^(2) ( \theta) = 1 -(0.866)^(2)`

`\cos^(2) ( \theta) = 0.250`

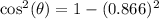
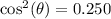
Take square root of both sides:

`\cos( \theta) = \pm √(0.250)`

`\cos( \theta) = \pm0.5`

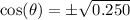
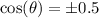
But we were given that:

`\pi \leqslant \theta \: \leqslant (3 \pi)/(2)`

which is the third quadrant and we know the cosine function is negative in this quadrant.

Hence

`\cos( \theta)= - 0.5`