Question

Find the point, M, that divides segment AB into a ratio of 5:6 if A is at (0,22) and B is at (11,0).

Answer 1

(5,12)

Explanation:

The co-ordinates of point M is

When provided with points A(x1, y1) and B(x2,y2) then to find the coordinates of the points that divide the line segment AB internally we use the formula

`X=\frac {mx1+nx2}{m+n} and y=\frac {my1+ny2}{m+n}`

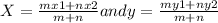
Similarly, for the same points but when it’s divided externally we use the formula

`X=\frac {mx1-nx2}{m-n} and y=\frac {my1-ny2}{m-n}`

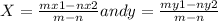
For this case, we use the first formula

M=5 and n=6 hence m+n=11

Total ratio is 5+6=11

Difference in x direction=11-0=11 points

Difference in y direction=0-22=-22 points

Point M=5/11(11, -22)+ point A

Point M=(5,-10)+(0+22)=(5,12)