Question

Given z=k/x^n find k and n if

X is 1 z 100
X is 2 z 25/2
X is 4 z ?
X is ? Z 3/25

Answer 1

n = - 3 and k = 100

Explanation:

We are given that
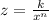`z = (k)/(x^(n) )` ......... (1) and we have to find k and n which are constants.

Now, from equation (1), we can write

`(z_(1) )/(z_(2) ) = ((k)/(x_(1) ^(n) ) )/((k)/(x_(2) ^(n) ))`

⇒
`(z_(1) )/(z_(2) ) = ((x_(2) )/(x_(1) ) )^(n)`

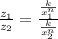
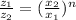
Now, for z = 100, x =1 and for z = 25/2, x = 2

Hence,
`(100)/((25)/(2) ) = ((1)/(2) )^(n) = 2^(-n)`

⇒
`2^(3) = 2^(-n)`

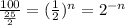
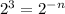
⇒ n = - 3

Now, from equation (1) we get

`z_(1) = (k)/(x_(1) ^(-3) )`

⇒
`100 = (k)/(1) = k`

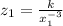
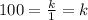
⇒ k = 100 {Since, x = 1, when z = 100}

Therefore, n = - 3 and k = 100 (Answer)