Question

How do you add all even numbers that are less than 123?

Answer 1

`61(61+1)=3782`

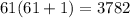
The formula for the sum of the first n positive evens is:

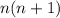`n(n+1)`. Your question is equivalent to what is the sum of the first 61 even positive integers.

Explanation:

122 is the highest even less than 123.

If we solve 2n=122 we can find what number term 122 is in the sequence of positive even numbers.

2n=122

Divide both sides by 2:

n=61

So 122 is the 61st positive even integer. This means we are adding 61 positive even integers.

2(1)+2(2)+2(3)+2(4)+2(5)+2(6)+..........+2(61)

Factor out out 2:

2(1+2+3+4+5+6+...+61)

We could write in summation notation if you prefer:

`2\sum_(k=1)^(61)k`

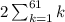
There is a formula for computing the following:

`\sum_(k=1)^(n)k=(n(n+1))/(2)`

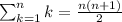
So we have the following:

`2(61(61+1))/(2)`

`61(61+1)`

`61(62)`

`3782`

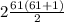
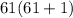
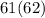
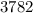
So if you wanted to know the sum of the first n even numbers it is:

`n(n+1)`.

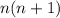Examples:

The sum of the first 4 positive even numbers:

`2+4+6+8=20`

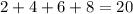
Now let's put our formula to the test:

`4(4+1)`

`4(5)`

`20`

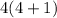
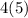
The sum of the first 10 positive even numbers:

`2+4+6+8+10+12+14+16+18+20=110`

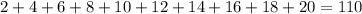
Now let's put out formula to the test again:

`10(10+1)`

`10(11)`

`110`

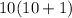
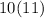
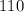
So as you can see the formula works.

Let me know if you want me to actually prove with mathematical induction.