Answer:
Explanation:
Let the length of the fence = x
Let the width of the fence = y
Recall that the perimeter of a rectangle is calculated by 2(L+B) , but the farmer is using the side of the barn on one side of the rectangle , so the perimeter equation is
x + 2y = 48
Area = xy
If we substitute the perimeter equation so that the area is only in terms of y.
Area = (48 - 2y)y
Area = 48y - 2
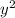
Now just find the vertex of the parabola
Area = -2
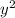 + 48y
+ 48y
A = -2
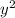 + 48
+ 48
Differentiate A with respect to y
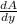 = -4y + 48
= -4y + 48
equate it to zero , we have
-4y + 48 = 0
4y = 48
y = 12
Substitute y = 12 into equation 1, we have
x = 48 - 2y
x = 48 - 2(12)
x = 48 - 24
x = 24
Therefore the dimensions of the garden are 24 by 12
The maximum area is 288 square unit