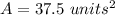Question

Helpppp!!!!!!!!!!!!!​

Answer 1

`A=37.5\ units^2`

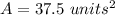
Explanation:

we know that

The area of a trapezoid is equal to

`A=(1)/(2)[b1+b2]h`

where

b1 and b2 are the parallel bases

h is the height of trapezoid (perpendicular distance between the two parallel bases)

In this problem the area is equal to

`A=(1)/(2)[BC+AD]AB`

we have the coordinates

`A(-3,2),B(1,5),C(7,-3),D(0,-2)`

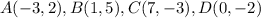
the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

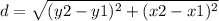
step 1

Find the distance AB

`A(-3,2),B(1,5`

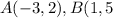
substitute in the formula

`d=\sqrt{(5-2)^(2)+(1+3)^(2)}`

`d=\sqrt{(3)^(2)+(4)^(2)}`

`d_A_B=5\ units`

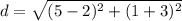
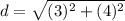
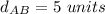
step 2

Find the distance BC

`B(1,5),C(7,-3)`

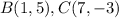
substitute in the formula

`d=\sqrt{(-3-5)^(2)+(7-1)^(2)}`

`d=\sqrt{(-8)^(2)+(6)^(2)}`

`d_B_C=10\ units`

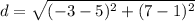
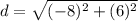
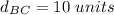
step 3

Find the distance AD

`A(-3,2),D(0,-2)`

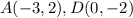
substitute in the formula

`d=\sqrt{(-2-2)^(2)+(0+3)^(2)}`

`d=\sqrt{(-4)^(2)+(3)^(2)}`

`d_A_D=5\ units`

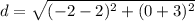
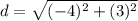
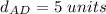
step 4

Find the area

`A=(1)/(2)[BC+AD]AB`

substitute the values

`A=(1)/(2)[10+5]5`

`A=37.5\ units^2`