Answer:
Distance between point
 and midpoint of line joining
and midpoint of line joining
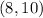 and
and
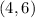 =
=
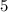 units.
units.
Explanation:
Given:
Points:
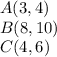
To find distance from point A to midpoint of BC.
Midpoint M of BC:
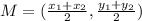
 [Plugging in points
[Plugging in points
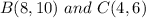 ]
]
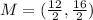
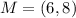
Distance between A and M:
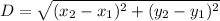
 [Plugging in points
[Plugging in points
 ]
]
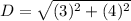
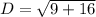
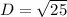
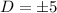
Since distance is always positive ∴
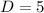 units
units