Question

Which equation represents a proportional relationship between the x and y values?

A) y = 2

B) y = 14x + 1

C) y = x − 4

D) y = −2x

Answer 1

The Anwser is D

Explanation:

Answer 2

D)
`y=-2x`

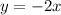
Explanation:

A linear relationship is of the form
`y=mx+b`, where,
`m` is the slope and
`b` is the y-intercept (constant).

For a proportional relationship, the value of
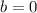`b=0` and thus it is of the form
`y=mx`

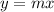
Let us check each option and express it in the form above.

Option A:

`y=2`

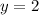
This can be written as
`y=0x+2`. So,
`b\\e 0`.

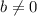Since, b \\e 0, therefore, it is not a proportional relationship.

Option B:

`y=14x+1`

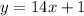
Here,
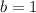`b=1`. So,
`b\\e 0`.

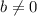Since, b \\e 0, therefore, it is not a proportional relationship.

Option C:

`y=x-4`

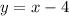
Here,
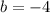`b=-4`. So,
`b\\e 0`.

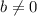Since, b \\e 0, therefore, it is not a proportional relationship.

Option D:

`y=-2x`

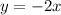
This can be rewritten as
`y=-2x+0`

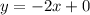
There is no y-intercept on this. So,
`b=0`

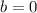
Since,
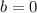`b = 0`, therefore, it is a proportional relationship.

Therefore, the correct option is D.