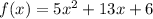Question

Use synthetic division to determine if x+2 is a factor of f(x)=5x2+13x+6

Answer 1

x+2 is a factor of
`f(x)  = 5x^2 + 13x + 6`

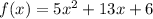
Explanation:

To check: If (x+2) is a a factor of the polynomial
`f(x)  = 5x^2 + 13x + 6`

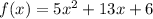
We need to check if x = -2 is the FACTOR of the given polynomial.

⇒ To show: f (-2) = 0

Now

`f(-2)  = 5(-2)^2 + 13(-2) + 6\\=5(4) -26 + 6\\= 20 + 6 - 26\\= 26 - 26  = 0\\\implies f(-2) = 0`

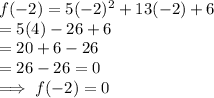
Since, f(-2) = 0

⇒ -2 is the ROOT of the Polynomial f(x).

⇒(x +2) is the factor of the given polynomial.

Hence, x+2 is a factor of
`f(x)  = 5x^2 + 13x + 6`