Answer:
Never. I don't know maybe this is a trick question.
Explanation:
a + x = 1 + a²x
Rearrange to look like standard form : ax² + bx + c = 0
0 = a + a²x - a - x
0 = a²x - x <= This is a quadratic equation.
Let's state the values of a, b and c.
a=a; b = -1; c = 0
INTERPRET THE FORMULA:
c represents the y-intercept.
When c is 0, the y-intercept is 0. The graph always passes through the origin.
Since the origin is (0,0) and is on the x-axis, the equation always has a solution: 0.
(solution = root = zero. It's when the graph passes through the x-axis.)
ALGEBRAICALLY:
The discriminant formula to find the number of solutions or roots in a graph is:
b² - 4ac.
When a quadratic has no solution, the discriminant equates to a negative number:
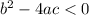 .
.
If it equates to 0, there is one solution.
If it equates to a number greater than 0, there are 2 roots.
Substitute the values into the discriminant formula. ( a=a; b = -1; c = 0 )
b² - 4ac
= (-1)² - 4(a)(0)
= 1 - 0
= 1
1 is greater than 0. It doesn't matter what a is.
Because a is multiplied with c=0, all of 4ac equates to 0, and is never greater than b², thus the entire formula will never equate to less than 0 to give the graph no solutions.