Answer:
A proportional relationship is there.
Explanation:
Here in the table, the values of y are given corresponding to the values of x.
There are four sets of values of x and y.
We have to check whether the relationship is proportional or not.
Now, rate of change of y with respect to x will be from the first two pair of values is =

Again, rate of change of y with respect to x will be from the second two pair of values is =
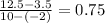
And, rate of change of y with respect to x will be from the third two pair of values is =
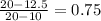
So, the rate is always 0.75.
Therefore, a proportional relationship is there. (Answer)