Answer:
It will be 290 years until there be one person for every square yard of land.
Explanation:
We are looking for when the country's population is equivalent to its area in square yards: 31,000,000,000.
Write an equation for the situation: (Trickiest part)
p(x) = (5,667,000)(1 + 0.022)ˣ <= Can modify compound interest equation
31,000,000,000 = (5,667,000)(1 .022ˣ)
Started rounding off numbers
547.056 = 1 .022ˣ <=
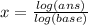
Solve using log.
x = 2.738 / 0.00945 <= log(547.056) / log(1.022)
x = 289.7 <= Round up because rate is annual. Before the 290th year, the population is less than the number of square yards.
x = 290
Total amount with annual compound interest equation applied to this problem:
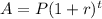 (Principle is starting investment)
(Principle is starting investment)
Population = (Starting population)(1 + growth rate)^(time)