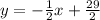Question

Determine the equation of a line in standard form that represents alanas training progress. Her progress points corresponds to the points (1,14) and (9,10)

Answer 1

The equation of the line passing through the above points is:

`y=-(1)/(2)x+(29)/(2)`

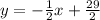
Explanation:

Given:

The two points are:
`(x_1,y_1)=(1,14)\textrm{ and }(x_2,y_2)=(9,10)`

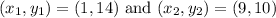
The equation of a line when two points are given is:

`y-y_1=\left ((y_2-y_1)/(x_2-x_1) \right )(x-x_1)`

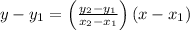
Plug in all the values and simplify.

`y-14=\left ((10-14)/(9-1) \right )(x-1)\\y-14=\left ((-4)/(8) \right )(x-1)\\y-14=-(1)/(2)(x-1)\\y-14=-(1)/(2)x+(1)/(2)\\y=-(1)/(2)x+(1)/(2)+14\\\\\\y=-(1)/(2)x+(29)/(2)`

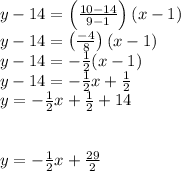
Therefore, the equation of the line passing through the above points is:

`y=-(1)/(2)x+(29)/(2)`