Answer:
A. { -20, -10, 20 }
Explanation:
Given:
The function is given as:
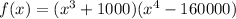
Let us simplify the function.
First, we use the identity
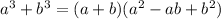
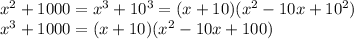
Next, we use the identity
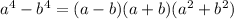

Now, the function can be rewritten as:
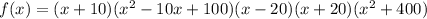
Now, the zeros are those values of
 for which
for which
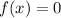
Now, for
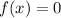 , we must have either of the factors 0.
, we must have either of the factors 0.
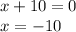
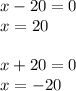
The factors
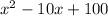 and
and
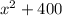 can have no zeros as the first one has imaginary roots and second one is always greater than 0 irrespective of the
can have no zeros as the first one has imaginary roots and second one is always greater than 0 irrespective of the
 values.
values.
So, the possible set of zeros are { -20, 10, 20 }.