Answer:
The area of sector with radius 3 cm and angle at center is
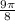 cm²
cm²
Explanation:
Given as :
The radius of circle = 3 cm
The angle at the center of circle = Ф =
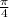 = 45°
= 45°
Now, Area of sector =
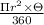
Or, Area of sector =
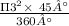
Or, Area of sector =
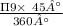
Or, Area of sector =
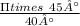
Or, Area of sector =
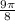 cm²
cm²
Hence The area of sector with radius 3 cm and angle at center is
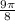 cm² Answer
cm² Answer