Answer:
∴ The angle of the vector is 49.4°.
Step-by-step explanation:
Given:
For a vector:
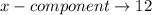
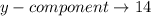
The tangent of angle of a vector is given by:
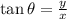
where
 represents the angle of the vector,
represents the angle of the vector,
 represents the length of
represents the length of
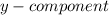 and
and
 represents the length of
represents the length of
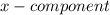 .
.
Plugging in the given values to get the angle of vector
 .
.
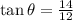
Taking
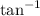 both sides to get
both sides to get

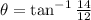
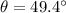
∴ The angle of the vector is 49.4°.