Question

The manager at the local auto shop has found that the probability that a car brought into the shop requires an oil change is 0.61​, the probability that a car brought into the shop requires brake repair is 0.39​, and the probability that a car requires both an oil change and brake repair is 0.12. For a car brought into the​ shop, determine the probability that the car will require an oil change or brake repair.

Answer 1

0.88

Explanation:

Let A be the event that a car brought into the shop requires an oil change

and B that a car brought into the shop requires brake repair

Given that

`P(A) = 0.61\\P(B)=0.39\\P(AB) = 0.12`

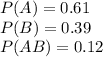
Here AB denotes both A and B

required probability = the probability that the car will require an oil change or brake repair

=P(AUB)

=P(A)+P(B)-P(AB)

=0.61+0.39-0.12

=0.88

Answer is 0,88 got by using addition theory of probability