Answer:
-
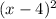
or -
 +8x-16
+8x-16
Explanation:
Given a second degree polynomial has a root 4 with multiplicity 2
That means, 4 is a repeating root of the polynomial.
Any second degree polynomial has at most 2 real roots.
⇒Both roots of the polynomial are 4.
and its expression can be written as c·
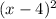 where c is a real number
where c is a real number
⇒c·(
 -8x+16)
-8x+16)
⇒c
 -8cx+16c
-8cx+16c
Also, the leading coefficient is given as -1
So, c = -1
and the expression becomes (-1)
 -8·(-1)·x+16·(-1)
-8·(-1)·x+16·(-1)
⇒-
 +8x-16
+8x-16