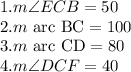Question

Match the following items.

If ∠DBC = 40°, then

1. m∠ECB =
40
2. m =
80
3. m =
50
4. m∠DCF =
100

Answer 1

1. m ∠DCF = 40

2. m ∠ECB = 50

3. m CD = 80

4. m BC = 100

Explanation:

Answer 2

`1. m\angle ECB=50\\2. m\textrm{ arc BC}=100\\3. m\textrm{ arc CD}=80\\4. m\angle DCF=40`

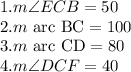
Explanation:

Given:

`\angle DBC=40`°

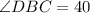From the triangle, using the theorem that center angle by an arc is twice the angle it subtend at the circumference.

`m\textrm{ arc CD}=2* \angle DBC\\m\textrm{ arc CD}=2* 40=80`

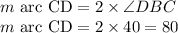
Also, the diameter of the circle is BD. As per the theorem that says that angle subtended by the diameter at the circumference is always 90°,

`m\angle BCD=90`

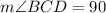
From the Δ BCD, which is a right angled triangle,

`m\angle DBC+m\angle BDC=90\textrm{ (right angled triangle)}\\40+m\angle BDC=90\\m\angle BDC=90-40=50`

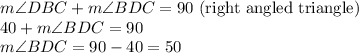
Now, using the theorem that angle between the tangent and a chord is equal to the angle subtended by the same chord at the circumference.

Here, chords CD and BC subtend angles 40 and 50 at the circumference as shown in the diagram by angles
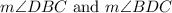`m\angle DBC\textrm{ and }m\angle BDC` and EF is a tangent to the circle at point C.

Therefore,
`m\angle DCF=m\angle DBC=40\\m\angle ECB=m\angle BDC=50`

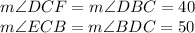
Again, using the same theorem as above,

`m\angle DCF=50\\\therefore m\textrm{ arc BC}=2* m\angle DCF=2* 50=100`

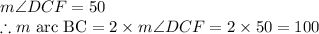
Hence, all the angles are as follows:

`1. m\angle ECB=50\\2. m\textrm{ arc BC}=100\\3. m\textrm{ arc CD}=80\\4. m\angle DCF=40`